오렌지 3로 배우는 통계와 데이터 분석
강사: 이숙번님
"표준편차"와 "확률"

- 집단에서 하나의 값을 꺼냈을 때, 그 값이
- 평균에서 1표준편차 사이 값일 확률. 68.2%
- 평균에서 2표준편차 사이 값일 확률. 95.4%
- 평균에서 3표준편차 사이 값일 확률. 99.6%
- 분포 그래프는 확률을 구하기 위한 그래프이다.
참고글: 지오지브라 그래프
https://www.geogebra.org/classic#probability
1. 이항 검정(Binomial Test)
: 이산 확률 분포를 따르는 데이터를 분석하기 위해 사용하는 통계적 검정 방법입니다.
- 특정 사건이 두 가지 결과로 나뉘는 경우, 관찰된 성공 횟수가 기대값과 얼마나 다른지를 검정하는 방법
- 이항분포를 이용한 검정
- N개 중에 K개를 맞췄을 때 찍어서 맞췄을 가능성

!pip install scipy
from scipy import stats
print(stats.binomtest(8, 10)) # 10개 중 8개 맞힐 확률
print(stats.binomtest(9, 10))
print(stats.binomtest(60, 100))
print(stats.binomtest(61, 100))
print(stats.binomtest(540, 1000))
# 결과
BinomTestResult(k=8, n=10, alternative='two-sided', statistic=0.8, pvalue=0.109375)
BinomTestResult(k=9, n=10, alternative='two-sided', statistic=0.9, pvalue=0.021484375)
BinomTestResult(k=60, n=100, alternative='two-sided', statistic=0.6, pvalue=0.056887933640980784)
BinomTestResult(k=61, n=100, alternative='two-sided', statistic=0.61, pvalue=0.03520020021770479)
BinomTestResult(k=540, n=1000, alternative='two-sided', statistic=0.54, pvalue=0.012444146277171822)
- 이항검정을 언제 사용하는가?
- 데이터가 두 가지 범주(예: 성공/실패)로 나뉠 때
- 샘플 크기가 작고 분포가 이항분포를 따를 때
2. T 검정(T-test)
: 모집단의 평균을 비교하기 위해 사용하는 통계적 검정 방법
- 주로 표본 크기가 작을 때 사용
- T분포를 이용한 검정 (자유도 = 샘플수 - 1)
- 두 집단의 숫자가 같은 모집단에서 뽑힌 숫자일 가능성
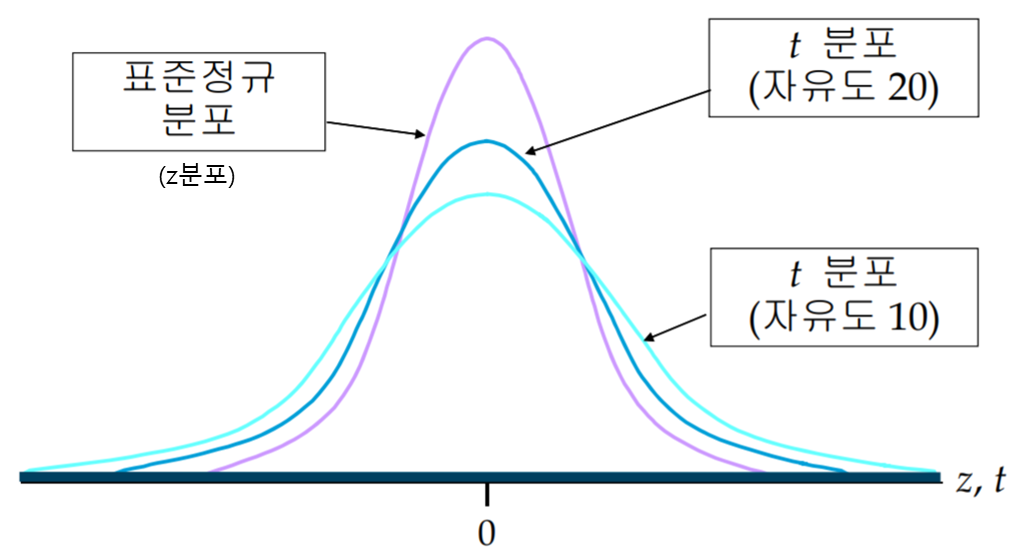
- T = 두 표본 평균의 차이 / 불확실성


⬛ 이용만 하면 되는 확률밀도함수와 검정

- T분포 / T검정
- 2개의 수치형 변수 간 차이 확인
- 카이 제곱 분포 / 카이 제곱 검정
- 범주형 변수 간 차이 확인
- F분포(Anova) 검정
- 3개 이상의 수치형 변수 간 차이 확인
※ 참고 글: 사이파이를 이용한 검정
- boxplot + p-value로 확인된 것
- 범주형 변수 : 범주형 변수 사이의 상관관계(O)
- 범주형 변수 : 수지형 변수 사이의 상관관계(X)
- 수치형 변수 : 수치형 변수 사이의 상관관계(X)
◼️ 수치형 변수 : 수치형 변수
- Scatter Plot
- 상관계수(Correlation)
- 1에 가까우면 양의 상관관계
- 0에 가까울수록 상관관계가 없음
- -1에 가까우면 음의 상관관계

변수사이의 상관관계는 BoxPlot, Correlations 위젯를 쓴다.
변수사이의 분포를 자세히 보고 싶으면 Distributions, Scatter Plot을 쓴다.
3. 평가지표 - 회귀


1. MSE (Mean Square Error)
- 에러의 제곱을 평균한다.
2.RMSE (Root Mean Square Error)
- MSE의 제곱근, 평균적인 오차값으로 해석할 수 있다.
3. MAE (Mean Absolute Error)
- 에러의 절대값을 평균한다
4. R2 - 평균과 비교하여 모델의 좋은 정도를 설명한다.
- 1이면 100점 모델
- 0이면 평균과 비슷한 수준
- 음수이면 평균보다 못한 모델
4. 평가지표 - 분류



1. AUC (Area Under The Curve)
- ROC(Receiver Operating Characteristics) 커브의 면적
- 클수록 좋은 모델
2. CA (Classification Accuracy) - 전체 정확도
3. Precision(정밀도) - 참으로 예측한 것 중 실제 참인 것의 비율
- 맞춘 확진자 / 확진자 전체
4. Recall(재현율) - 실제 참을 참으로 예측한 비율
- 맞춘 확진자 / 확진 예측 전체
5. F1 Score - Precision, Recall의 조화 평균
- 데이터가 편중되어 있을 때 한 쪽 쏠림 예측에 대해 확인
⬛ 정밀도(Precision)
: 모델이 양성(Positive)으로 예측한 사례 중 실제로 양성(True Positive)인 사례의 비율을 나타냄.
- 게산식: 정밀도 = TP / (TP + FP)
- 정밀도가 높을 수록 모델이 양성으로 예측할 결과의 정확도가 높음을 의미함.
즉, 모델이 잘못된 양성 예측을 얼마나 줄였는지를 평가할 수 있음
⬛ 재현율(Recall)
: 실제 양성인 사례 중 모델이 양성으로 정확히 예측한 비율을 나타냄.
- 계산식: 재현율 = TP / (TP + FN)
- 재현율이 높으수록 모델이 실제 양성인 사례를 놓치지 않고 잘 찾아냈을 의미함.
즉, 모델이 실제 양성 사례를 얼마나 잘 검출하는 지를 평가할 수 있음.
⬛ F1-Score
: 머신러닝 분류 모델의 성능를 평가하는 지표
- 정밀도와 재현율의 조화 평균을 나타냄.
- 모델이 얼마나 정확하게 예측하는 지와 실제 양성 데이터를 얼마나 잘 찾아내는 지를 고려함.

- 계산식: F1 스코어 = 2 * (정밀도 x 재현율) / (정밀도 + 재현율)
- F1 스코어는 0과 1사이의 값을 가지며, 1에 가까울 수록 모델의 성능이 우수함.
특히 데이터의 클래스 불균형이 심한 경우 정확도(Accuracy)보다 F1 스코어가 모델의 성능을 평가하는데 더 유용함.
예시: 스팸 이메일 분류 모델
- 정밀도가 높다면, 스팸으로 예측한 이메일 중 실제 스팸의 비율이 높음을 의미함.
- 재현율이 높다면, 실제 스팸 이메일 중 모델이 스팸으로 정확히 예측한 비율이 높음을 의미함.
- F1 스코어는 이 두 지표의 균형을 평가하여 모델의 전반적인 성능을 나타냄
-> F1 스코어는 모델이 양성 클래스에 대해 얼마나 정확하고 포괄적으로 예측하는 지를 종합적으로 평가하는데 유요한 지표임.
내용은 계속 업데이트하도록 하겠습니다.
출처: AI Hub 교육과정 - WEB+AI (위 내용이 문제가 된다면 댓글에 남겨주세요. 바로 삭제조치하도록 하겠습니다.)
'Programming 개발은 구글로 > 기타 정보' 카테고리의 다른 글
| [WEB+AI] 25일차 Orange 3 통계 - Logistic Regression, Tree 모델 (6) | 2024.11.15 |
|---|---|
| [WEB+AI] 24일차 오렌지 3 통계 3/3 (1) | 2024.11.15 |
| [WEB+AI] 22일차 오렌지 3 통계 1/3 (1) | 2024.11.12 |
| [WEB+AI] 21일차 머신러닝 (0) | 2024.11.11 |
| [WEB+AI] 20일차 Orange 3를 이용한 데이터 사이언스 입문 (7) | 2024.11.08 |




댓글