오렌지 3 통계
강사: 이숙번님
1. 통계의 목적: 이해와 예측
1. 기술 통계(이해) - 수집된 데이터의 요약과 설명
a. 데이터를 한 개의 대표값으로 표현하기
b. 흩어짐의 정도로 데이터 이해하기(분포)
2. 추론 통계(예측) - 기술 통계 결과를 기반으로 일반화, 예측, 추정
a. 모집단을 표본으로 추정해보기
b. 가설을 검증해가며 데이터를 파악해가기
- 기술 통계의 기초 레시피 5개
a. 평균
b. 표준편차
c. 중앙값
d. 사분위수
e. 최빈값

1.1. 평균
: 보통의 값 = "최초의 예측 모델"
- 집단을 잘 표현하는 하나의 숫자(대푯값)을 가짐.
- 집단을 비교할 수 있게 됨.
예제)
- 대한민국 사람을 아무나 한 명 선택했을 때 그 사람의 키는?
- 내일은 레모네이드가 얼마나 팔릴까?
- 다음 경기에 A선수를 기용하면 얼마의 득점을 할 것인가?
-> 비교는 이해를 위한 핵심이다.
- 비교(평균) 다음은? 질문이고, 질문의 답을 찾는 것이 이해(예측모델)이다.
1.2. 표준편차
: 평균으로부터의 거리, 편차들의 평균
- 집단이 어떻게 분포되어 있는지를 표현하는 숫자(대푯값)입니다.
- 집단의 분포된 정도를 비교할 수 있게 됨.
예제)
- A반에서 임의로 선택한 학생의 성적이 90점 이상일 확률은?
- 내일 레모네이드가 10잔 이상 팔릴 확률은?
- A선수를 기용했을 때, 10점 미만으로 득점할 확률은?
1.3. 중앙값
: 평균의 대체재
- 이상치는 평균의 대표성을 무너뜨린다.
예제)
[1, 2, 3, 4, 5, 7, 100] 평균: 17.42
[1, 2, 3, 4, 5, 7, 10] 평균: 4.57
- 평균이 대표값의 역활을 못할 때 중앙값을 사용함.
- 값을 정렬한 후에 가장 가운데에 있는 값이 중앙값.
수식
: 홀수 일 때 가운데 값을 가져오고, 짝수이면 가운데 값이 2개가 나오는데, 그 값의 평균.

1.4. 사분위수
: 표준편차의 보완

- 평균과 표준편차
- 통계를 떠받치고 있는 기초이다
- 합계를 통한 요약
- 장점: 값의 중심. 용이함
- 단점: 이상치에 취약
- 중앙값과 사분위수
- 정렬을 통한 요약
- 평균과 표준편차 약점 보완
- 장점: 이상치에 강함
- 단점: 편차를 충분히 설명 못함
1.5. 최빈값과 빈도수
: 최빈값은 가장 많이 등장하는 값이다.
- 수치형이 아닌 범주형일 경우 최빈값으로 확인함.
- 빈도수를 체크하여 확인함.
- 데이터의 유형
- 범주형: 카테고리를 나눔
- 명목형 / 순서형
- 수치형: 수량을 의미함
- 연속형 / 이산형

집단의 비교는 쉽지 않다.
두 개의 맛이 다른가?
MIF vs TIF(베르누이 시행)
두 집은 다른가?
A반 수학 평균 70점, B반 수학 평균 75
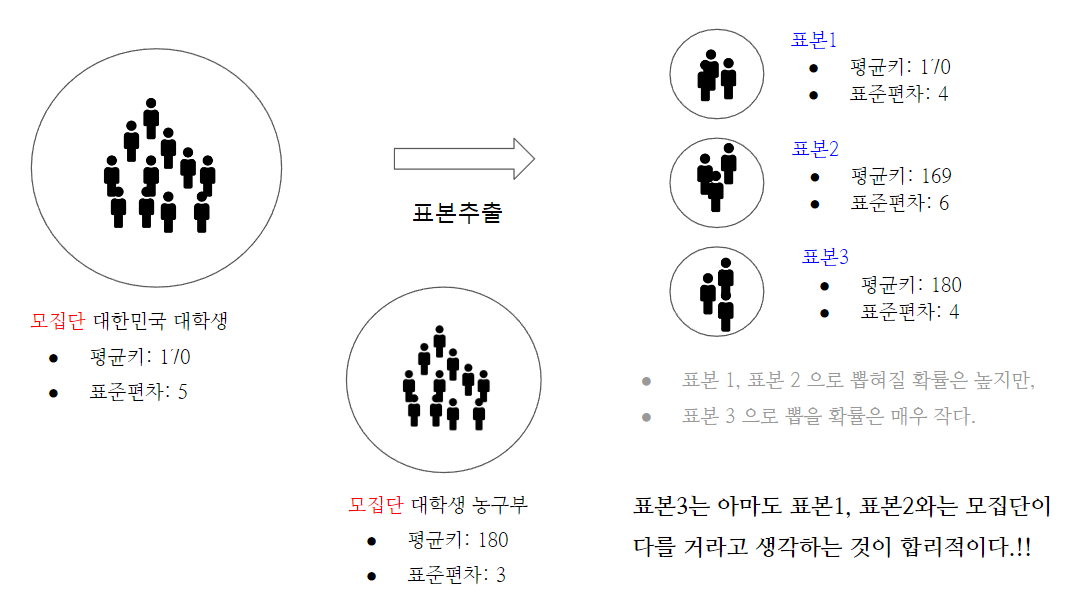
- 질문을 확률 문제로 바꿔야 합니다.
- 두 개의 맛은 다른가? (두 맛의 차이를 아는가?)
- 두 집단은 다른가?
- 집단이 같은 모집단이면 집단의 구분은 의미가 없다.(상관관계가 없다.)
- 서로 같은 모집단에서 뽑았을 확률이 적으면 상관관계가 있다.

- 가설 검증
- 귀무가설(null hypothesis, HO)
- 보수적인 입장, 차이가 없다. 변화가 없다. 등등
- p-value > 0.05 일 때 귀무가설 채택
- 대립가설(alternative hypothesis, H1)
- 우리가 바라는 무언가, 차이가 있다. 변화가 있다. 등등
- p-value <= 0.05 일 때 대립가설 채택
- 사건이 우연히 발생할 확률로 평가
- 아무 관계도 아닌 두 사람이
- 길거리에서 3번 발견되는 확률이
- 5% 미만이라는 것을 확인. (p-value)
두 사람이 3번 발견된 사건은 사귀는 관계일거야. (사귀는 관계에 대해 통계적으로 유의하다.)
출처: AI Hub 교육과정 - WEB+AI (위 내용이 문제가 된다면 댓글에 남겨주세요. 바로 삭제조치하도록 하겠습니다.)
'Programming 개발은 구글로 > 기타 정보' 카테고리의 다른 글
| [WEB+AI] 24일차 오렌지 3 통계 3/3 (1) | 2024.11.15 |
|---|---|
| [WEB+AI] 23일차 오렌지 3 통계 2/3 (1) | 2024.11.15 |
| [WEB+AI] 21일차 머신러닝 (0) | 2024.11.11 |
| [WEB+AI] 20일차 Orange 3를 이용한 데이터 사이언스 입문 (7) | 2024.11.08 |
| [WEB+AI] 19일차 사생대회 + 파이썬 (2) | 2024.11.07 |




댓글